Data Science in Finance

Lousy models are great!

The answer might surprise you!

Hungry for coin flips?

What's your $R^2$?

Our model:

$$ \begin{align*} Y =& \begin{cases} 1 & \text{ if "heads"} \\ 0 & \text{ if "tails"} \end{cases} \\ P(Y=1) =& w \\ \hat Y \equiv& 1 \end{align*} $$

$$ \begin{align*} \text{SSE} =& \sum\limits_{i=0}^{n-1}\left(y_i - \hat y_i\right)^2 & \text{SST} =& \sum\limits_{i=0}^{n-1}\left(y_i - \bar y\right)^2 \\ =& \sum\limits_{i=0}^{n-1}\left(y_i - 1\right)^2 & =& \sum\limits_{i=0}^{n-1}\left(y_i - 0.5\right)^2 \\ =& \sum\limits_{i=0}^{n-1}\left(y_i^2 -2y_i + 1^2\right) & =& \sum\limits_{i=0}^{n-1}\left(y_i^2 - 2(0.5)y_i + 0.5^2\right) \\ =& \sum\limits_{i=0}^{n-1}\left(-y_i + 1\right) & =& \sum\limits_{i=0}^{n-1}\left(0.25\right) \\ =& -nw + n & =& 0.5n \\ =& n(1-w) & =& 0.5n \\ \end{align*} $$

So, our $R^2$ is:

$$ \begin{align*} R^2 =& 1 - \frac{\text{SSE}}{\text{SST}} \\ =& 1 - \frac{n(1-w)}{0.5n} \\ =& 2w - 1 = 1.1 - 1 = 0.1 \end{align*} $$

Not necessarily bad Data Scientists

So what are the bets we're making?

Not just making money

Finding which stocks will go up is pretty much a solved problem. Most "secure" stocks will rise in price on a long enough time-line. But just because the total price of stocks in your account has risen doesn't mean the value has risen. You have to account for the value of money (which is constantly dropping -- inflation).

To illustrate this: we could make money by investing in General Electric in 2010 and holding our stock.

If we'd done that, we would have seen on average about 6% return per year! That's over the average inflation of somewhere between 3-5 percent, so we're looking pretty good, right?

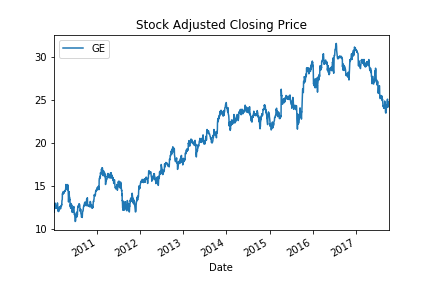
Looking good?

Well, yes and no. On the one hand, we did make money (at the expense of some risk, of course). But what if we'd chosen a better company to invest in like Apple? Or what if we'd invested instead in an index fund like Spyder?

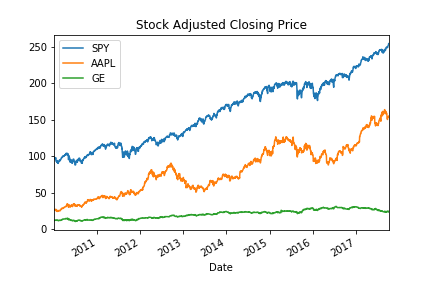
Better yet!

We can continue this thought process ad infinitum. For instance, we could've invested in Google. Or done something even crazier (a plot I won't show for simplicity reasons) -- volatility trading.

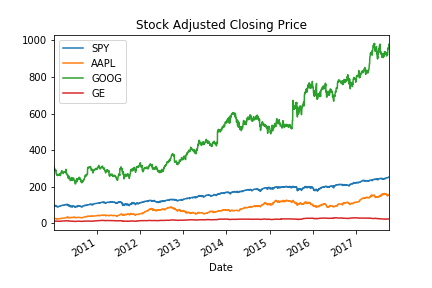
So what's the game?

Active Portfolio Management

Richard C. Grinold, Ronald N. Kahn

The Hedge Fund Mission

Make money

Like Roulette

A paraphrasing

The CAPM

Capital Asset Pricing Model

Risk

What is it?

Variance?

Exceptional Returns